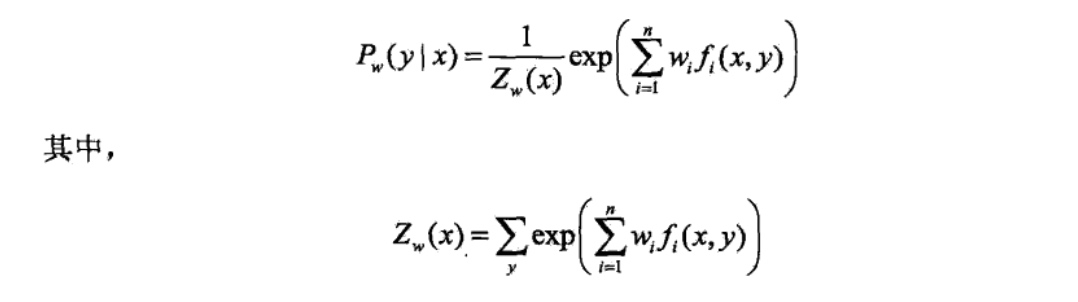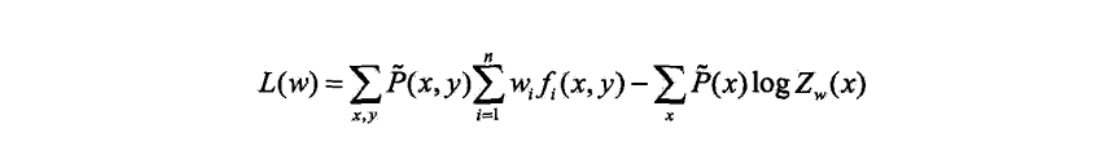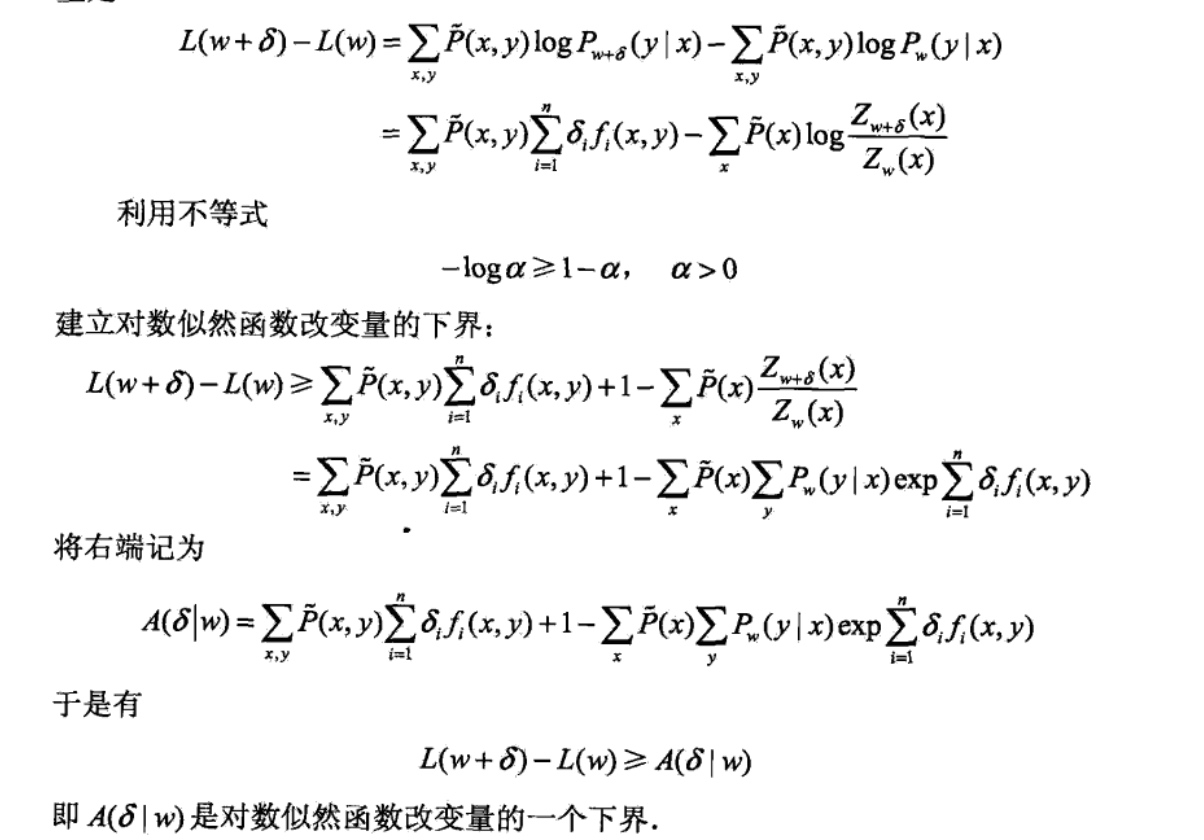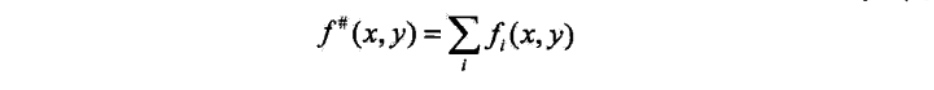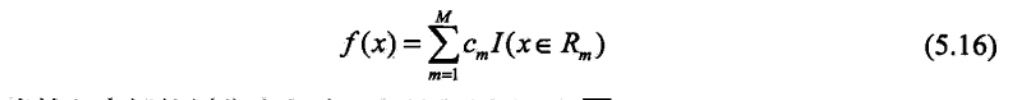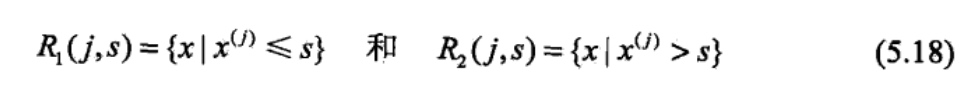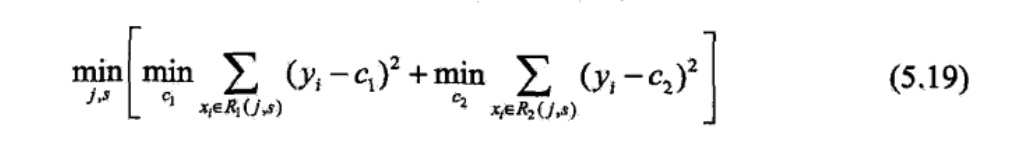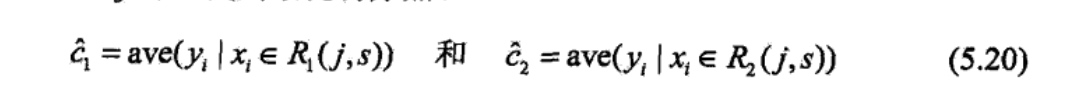图像去雾相关基础

暗原色

暗原色先验理论指出，在无雾图像的 非天空区域里，若把图像分为多个子块，则在每个子块中都会 有某些像素点的一个颜色通道的亮度接近于 0



HSV

HSL 和 HSV（也叫做 HSB）是对RGB 色彩空间中点的两种有关系的表示，它们尝试描述比 RGB 更准确的感知颜色联系，并仍保持在计算上简单。HSL 表示hue（色相）、saturation（饱和度）、lightness（亮度），HSV 表示 hue、 saturation、value(色调) 而 HSB 表示hue、saturation、brightness（明度）。

HSL 和 HSV 二者都把颜色描述在圆柱体内的点，这个圆柱的中心轴取值为自底部的黑色到顶部的白色而在它们中间是的灰色，绕这个轴的角度对应于“色相”，到这个轴的距离对应于“饱和度”，而沿着这个轴的距离对应于“亮度”，“色调”或“明度”。

HSV（色相，饱和度，明度）在概念上可以被认为是颜色的倒圆锥体（黑点在下顶点，白色在上底面圆心）
2017/5/4 posted in  图像去雾技术

图像去雾相关论文总结

  • 2.尺度自适应暗通道先验去雾方法

    1.特征学习的单幅图像去雾算法 2016年

    目的：为提高图像去雾的普适性，提出一种特征学习的单幅图像去雾方法。

    方法：通过稀疏自动编码机对有雾图像进行多尺度的纹理结构特征提取，同时抽取各种与雾相关的颜色特征。然后采用多层神经网络进行样本训练，得到雾天条件下纹理结构特征及颜色特征与场景深度间的映射关系，并估算出有雾图像的场景深度图。最后结合大气散射模型，根据场景深度图复原无雾图像。

    结论：对实验结果的定性及定量分 析表明，本文算法能有效获取有雾图像的场景深度，复原出视觉效果理想的无雾图像，且具有很好的场景普适性。

    理解：本文认为图像去雾的问题可进一步转化为场景深度d的求解问题。本文通过自动编码机获取到图片中物体的纹理特征，然后用多尺度的方法分别提取颜色特征、暗原色特征、颜色衰减特征、纹理结构特征。四者结合对场景深度进行估计。

    可以改进的：

    1. 算法实时性不够强，效率比较低，可以考虑缩小图片尺寸，降低数据量，从而运用到视频去雾。

    2. 对雾气分布不均匀的图像，效果不理想，需要结合不同的气象模型来建立更为鲁棒的物理模型。

    2.尺度自适应暗通道先验去雾方法

    目的：
    针对暗通道先验去雾方法的尺度选择问题 提出了一种尺度自适应方法， 根据图像的颜色和边 缘特征将暗通道求解的尺度自适应地调整到一个合适的范围。

    方法：

    1. 由颜色特征求解初始尺度：对于图像的不同区域采用不同的尺度求解暗通道: 在亮度较低或饱和度较高的区域，采用较小尺度; 在亮度较高且饱和度较低的区域，采用较大尺度;在景深突变处，采用较小尺度;在平滑区域，采用较大尺度。

    2. 由边缘特征对尺度进行修正:由于“光晕”现象发生在景深突变处，如果在边缘附近采用较小的尺度，可使透射率的求解窗口\(Ω_r(x)\)尽量不跨越景深边界，从而减小“光晕”现象; 在非边缘处采用较大的尺度，可以增大 \(J_{dark}(x)→0\)的概率，使复原图像的背景更平滑，噪声和失真更小。 由边缘特征对初始尺度\(r_0(x)\)进行修正.

    结论：
    整个去雾过程参数自动配置，无需人工干预，兼顾不同尺度复原图像的优点，复原图像色彩自然，对比度提升显著，并有效抑制了“光晕”现象。对多种雾化场景图像的处理结果表明: 文中方法对场景的适应性强， 在任何情况下的处理结果均能达到 DG 方法的最优结果，甚至更好。

    理解：
    该论文主要是针对HE的去雾方法，对暗通道尺寸进行自适应确定，减少了人工干预的复杂度。

    可以改进：
    该算法在运行时间上可以改进，也可以利用机器学习的方法来提取图片特征，避免Canny算子的局限性造成的边缘提取误差。
    可以与上篇论文进行结合来提高上文尺度特征提取的效率。

    • 2017/4/27 posted in  图像去雾技术

    文档测试

    如果你经常阅读Python的官方文档，可以看到很多文档都有示例代码。比如re模块就带了很多示例代码：

    >>> import re
>>> m = re.search('(?<=abc)def', 'abcdef')
>>> m.group(0)
'def'

    可以把这些示例代码在Python的交互式环境下输入并执行，结果与文档中的示例代码显示的一致。

    这些代码与其他说明可以写在注释中，然后，由一些工具来自动生成文档。既然这些代码本身就可以粘贴出来直接运行，那么，可不可以自动执行写在注释中的这些代码呢？

    答案是肯定的。

    当我们编写注释时，如果写上这样的注释：
    2017/4/22

    模型学习的最优化算法（接上一文）

    逻辑斯谛回归模型、最大嫡模型学习归结为以似然函数为目标函数的最优化问题，通常通过迭代算法求解.从最优化的观点看，这时的目标函数具有很好的性质.它是光滑的凸函数，因此多种最优化的方法都适用，保证能找到全局最优解.常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法.牛顿法或拟牛顿法一般收敛速度更快.

    这次主要学习基于改进的迭代尺度法与拟牛顿法的最大熵模型学习算法。（还有梯度下降法，这次不过多学习）

    改进的迭代尺度法

    改进的迭代尺度法（improved iterative scaling，IIS)是一种最大熵模型学习的最优化算法.

    已知最大熵模型为：

    对数似然函数为：

    目标是通过极大似然估计学习模型参数，即求对数似然函数的极大值\(\hat{w}\)

    改进的迭代尺度算法（iis）的想法是：假设最大熵模型当前的参数向量是\(w=(w_1,w_2,...,w_n)^T\),我们 希望找到一个新的参数向量\(w+\delta = (w_1+\delta_1,w_2+\delta_2,....,w_n+\delta_n)^T\)，使得模型的对数似然函数值增大.如果能有这样一种参数向量更新的方法\(\tau:w \rightarrow w+\delta\),那么就 可以重复使用这一方法，直至找到对数似然函数的最大值.

    对于给定的经验分布\(\tilde P(x,y)\),模型参数从\(w到w+\delta\)，对数似然函数的改变量是：

    如果能找到适当的\(\delta使下届A(\delta | w)\)提高，那么对数似然函数也会提高。然而，函数\(A(\delta | w)\)中的\(\delta\)是一个向量，含有多个变量，不容易同时优化，IIS试图以此只优化其中一个变量\(\delta_i\)，而固定其他变量\(\delta_j,i \neq j\).

    为达到这一目的，IIS进一步降低下界\(A(\delta | w)\),具体的，IIS引进一个量\(f^{\#}(x,y)\):

    因为\(f_i\)是一个二值函数，故\(f^{\#}(x,y)\)表示所有特征在（x，y）出现的次数，这样，\(A(\delta | w)\)可以改写为：

    下面给出IIS算法：

    2017/4/13

    logistic regression(逻辑斯蒂回归)

  • 最大熵模型

    简介：逻辑斯谛回归（logistic regression)是统计学习中的经典分类方法.最大熵是 概率模型学习的一个准则，将其推广到分类问题得到最大熵模型(maximum entropy model).逻辑斯谛回归模型与最大熵模型都属于对数线性模型.

    逻辑斯蒂回归模型

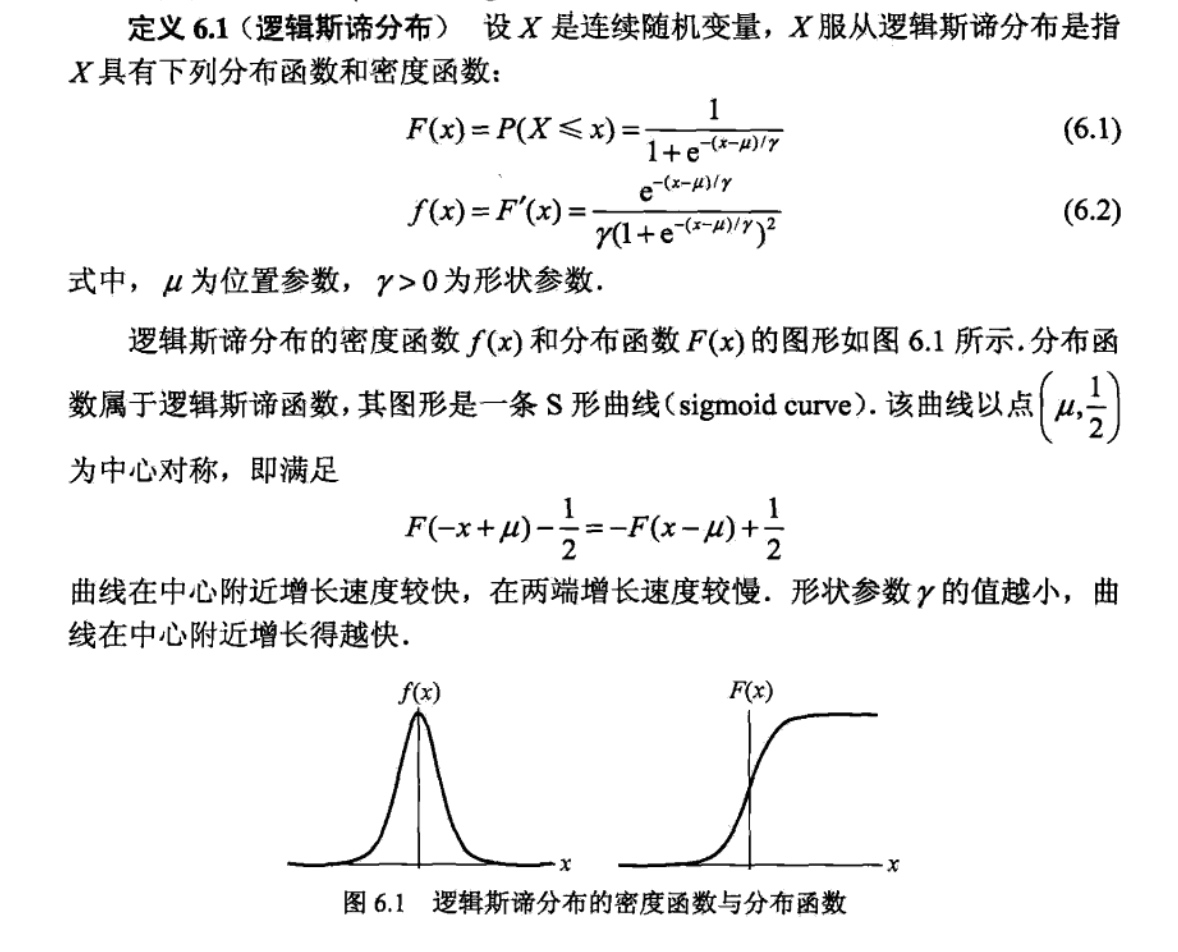
    逻辑斯蒂分布

    二项逻辑斯蒂回归模型

    二项逻辑斯诗回归模型（binomial logistic regression model)是一种分类模型，由条件概率分布\(P(Y|X)\)表示，形式为参数化的逻辑斯谛分布.这里，随机变量X取值为实数，随机变量Y取值为1或0.我们通过监督学习的方法来估计模型参数.


    现在考査逻辑斯谛回归模型的特点.一个事件的几率（odds)是指该事件发生的概率与该事件不发生的概率的比值.如果事件发生的概率是p,那么该亊件的几率是\(\frac{1}{1-p}\) ,该事件的对数几率(log odds)或logit函数是

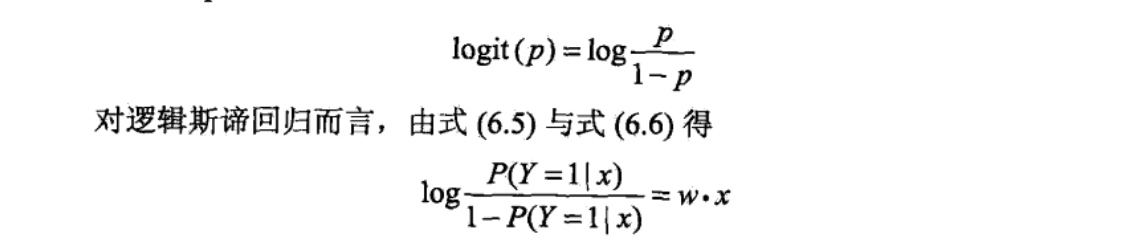
    这就是说，在逻辑斯谛回归模型中，输出y = l的对数几率是输入x的线性函数.或者说，输出Y=1的对数几率是由输入x的线性函数表示的模型，即逻辑斯谛回归模型.

    换一个角度看，考虑对输入x进行分类的线性函数\(w*x\),其值域为实数域.注意，这里\(x\in R^{n+1},w \in R^{n+1}\).通过逻辑斯谛回归模型定义式(6.5)可以将线性函数\(w*x\)转换为概率：

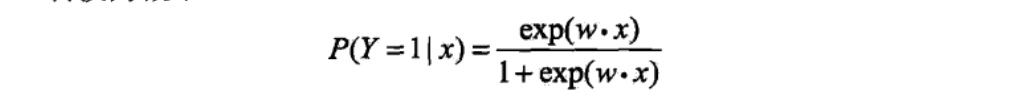
    这时，线性函数的值越接近正无穷，概率值就越接近1；线性函数的值越接近负无穷，概率值就越接近0(如图6.1所示).这样的模型就是逻辑斯谛回归模型.

    模型参数估计

    逻辑斯谛回归模型学习时，对于给定的训练数据集\(T=\{{(x_1,y_1),(x_2,y_2)...(x_N,y_N)\}}\),其中\(x_i\in R^n,y_i \in \{{0,1\}}\)，可以应用极大似然估计法估计模型参数，从而得到逻辑斯谛回归模型.

    多项了逻辑斯蒂回归

    上面介绍的逻辑斯谛回归模型是二项分类模型，用于二类分类.可以将其推广为多项逻辑斯缔回归模型(multi-nominal logistic regression model)，用于多类分类.假设离散型随机变量Y的取值集合是{1,2...K}，那么多项逻辑斯谛回归模型是:

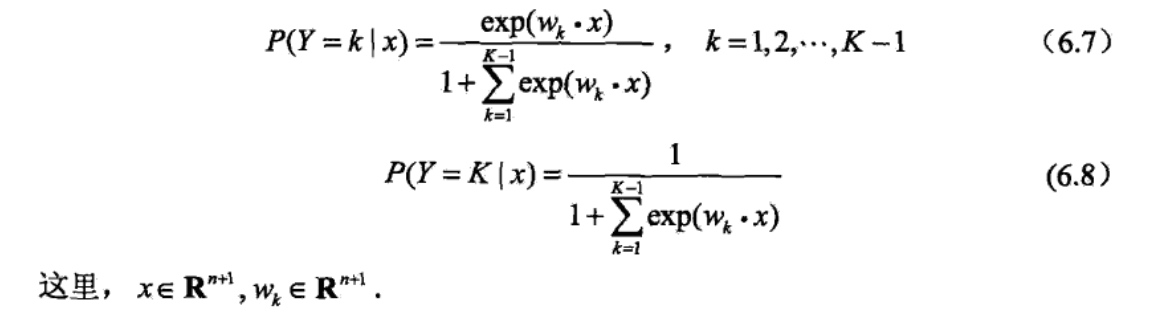
    二项逻辑斯谛回归的参数估计法也可以推广到多项逻辑斯讳回归.

    最大熵模型

    最大熵模型（maximum entropy model)由最大熵原理推导实现.这里首先叙述一般的最大熵原理，然后讲解最大熵模型的推导，最后给出最大熵模型学习的形式。

    最大熵原理

    最大熵原理是概率模型学习的一个准则.最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型.通常用约束条件来确定概率模型的集合，所以，最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型.

    假设离散随机变量X的概率分布是p(X),则其熵是：

    直观地，最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件.在没有更多信息的情况下，那些不确定的部分都是“等可能的”.最大熵原理通过熵的最大化来表示等可能性.“等可能”不容易操作，而熵则是一个可优化的数值指标.

    首先，可以通过一个简单的例子来了解一下最大熵原理.

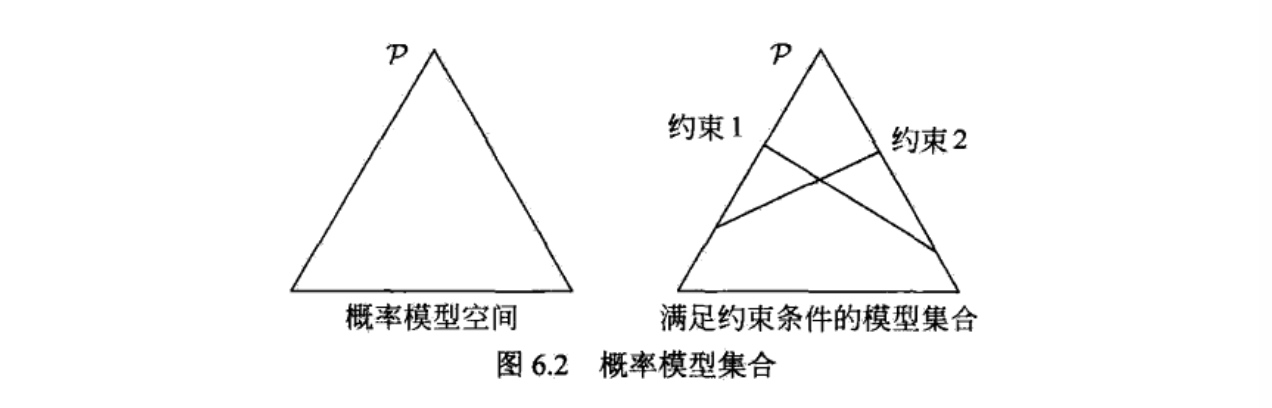
    图6.2提供了用最大熵原理进行概率模型选择的几何解释.概率模型集合P可由欧氏空间中的单纯形(simplex)表示，如左图的三角形(2-单纯形).一个点代表一个模型，整个单纯形代表模型集合.右图上的一条直线对应于一个约束 条件，直线的交集对应于满足所有约束条件的模型集合.一般地，这样的模型仍有无穷多个.学习的目的是在可能的模型集合中选择最优模型，而最大熵原理则给出最优模型选择的一个准则.

    最大熵模型的定义

    最大熵原理是统计学习的一般原理，将它应用到分类得到最大熵模型.

    假设分类模型是一个条件概率分布\(P(Y|X),X \in \mathcal{X} \subseteq R^n\)表示输入，\(Y \in \mathcal{Y}\)表示输出，\(\mathcal{X}\)和\(\mathcal{Y}\)分别是输入和输出的集合.这个模型表示的是对于给定的输入\(\mathcal{X}\)，以条作概率\(P(Y|X)\)输出Y.
    给定一个训练数据集
    \(T= {\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)}\}\)
    学习的目标是用最大熵原理选择最好的分类模型。

    首先考虑模型应该满足的条件，给定训练数据集，可以确定联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布，分别以\(\tilde{P}(X,Y)和\tilde{P}(X)\)表示。这里：

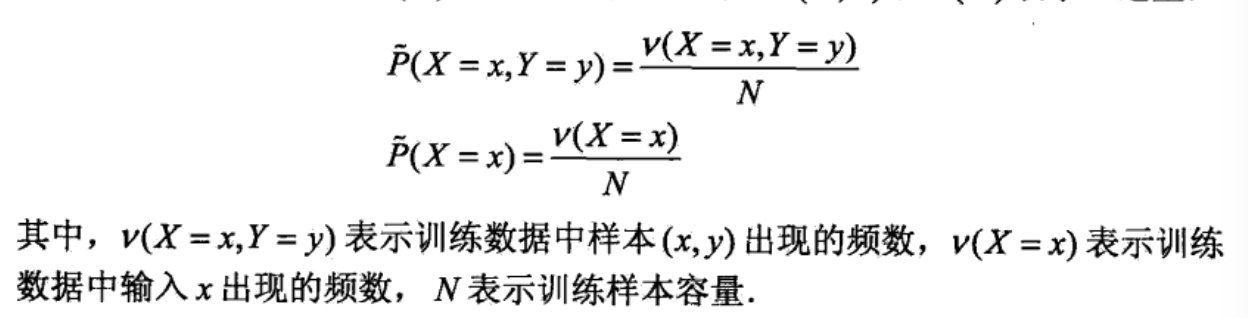
    用特征函数\(f(x,y)描述输入x和输出y之间的某一个事实\)。其定义是：

    特征函数f(x,y)关于经验分布\(\tilde{P}(X,Y)\)的期望值，用\(E_\tilde{P}(f)\)表示：

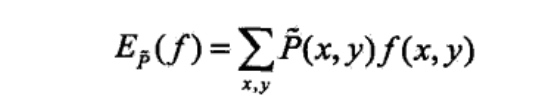
    特征函数f(x,y)关于模型P(Y|X)与经验分布\(\tilde{P}(X)\)的期望值，用\(E_{P}(f)\)表示：

    最大熵模型的定义为：

    最大熵模型的学习

    最大熵模型的学习过程就是求解最大熵模型的过程.最大熵模型的学习可以形式化为约束最优化问题.
    对于给定的训练数据集\(T= {\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)}\}\)以及特征函数\(f_i(x,y),i=1,2,...n\),最大熵模型的学习等价于约束最优化问题：

    求解约束最优化问题(6.14)〜(6.16)，所得出的解，就是最大熵模型学习的解.下面给出具体推导.
    这里，将约束最优化的原始问题转换为无约束最优化的对偶问题.通过求解对偶问题求解原始问题.

    下面举例来说明最大熵模型的计算：

    例：假设随机变量X有5个取值{A,B,C,D,E}，要估计各个值的概率P(A),P(B),P(C),P(D),P(E).



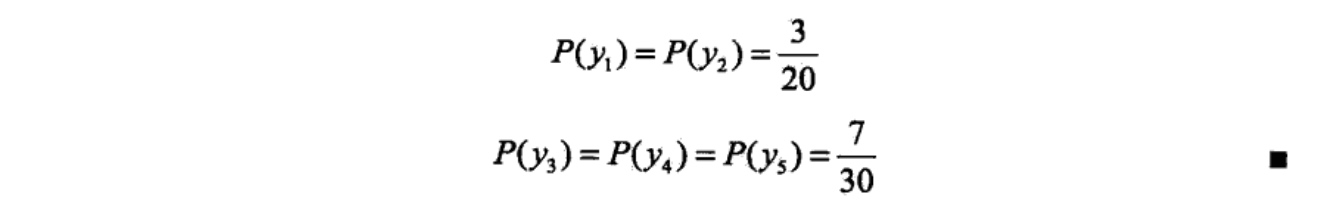
    极大似然估计

    从以上最大熵模型学习中可以看出，最大熵模型是由式(6.22)、式(6.23)表示的 条件概率分布.下面证明对偶函数的极大化等价于最大嫡模型的极大似然估计.

    己知训练数据的经验概率分布\(\tilde{P}(X,Y)\),条件概率分布\(P(Y|X)\)的对数似然 函数表示为:

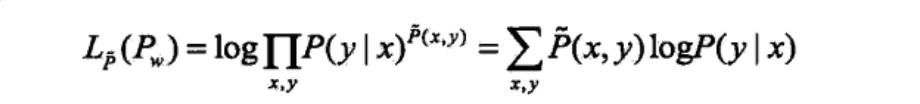
    当提哦啊煎概率分布P(y|x)是最大熵模型(6.22)和(6.23)时,对数似然函数\(L_ \tilde{p}(P_w)\)为：

    比较算式(6.26)和式(6.27),可得：

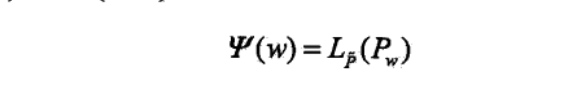
    既然对偶函数\(\psi(w)\)等价于对数似然函数\(L_{\tilde p}(P_w)\) ,于是证明了最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计这一事实.
    这样，最大熵模型的学习问题就转换为具体求解对数似然函数极大化或对偶函数极大化的问题.

    可以将最大熵模型写成更一般的形式.

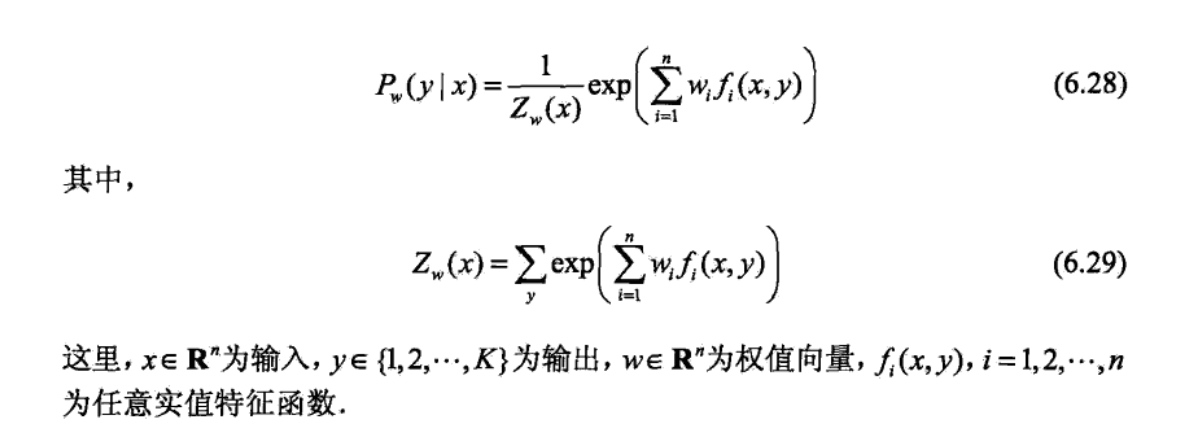
    最大熵模型与逻辑斯谛回归模型有类似的形式，它们又称为对数线性模型(log linear model).模型学习就是在给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计.

    • 2017/4/10

    决策树生成--CART算法

    CART算法

    分类与回归树(classification and regression tree, CART)模型由 Breiman等人在1984年提出，是应用广泛的决策树学习方法.CART同样由特征选择、树 的生成及剪枝组成，既可以用于分类也可以用于回归.以下将用于分类与回归的树统称为决策树.

    CART是在给定输入随机变量X的条件下输出随机变量Y的条件概率分布的学习方法.CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支.这样的决策树等价于递归地二分每个特征，将输入空间即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布.

    CART算法由以下两步组成：

    1.决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大：
    2.决策树剪枝：用验证数据集对己生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准.

    CART生成

    决策树的生成就是递归地构建二叉决策树的过程.对回归树用平方误差最小化准则，对分类树用基尼指数(Gini index)最小化准则，进行特征选择，生成二叉树.

    1.回归树的生成

    假设X与Y分别为输入和输出变量，并且Y是连续变量，给定训练数据集:
    \(D={(x_1,y_1),(x_2,y_2),...(x_N,y_N)}\)
    考虑如何生成回归树。

    一个回归树对应着输入空间（即特征空间）的一个划分以及在划分的单元上 的输出值.假设己将输入空间划分为M个单元\(R_1,R_2,R_3...R_M\),并且在每个单元\(R_M\)上 有一个固定的输出值\(c_m\)，于是回归树模型可表示为:

    当输入空间的划分确定时，可以用平方误差\(\sum_{x_i\in R}(y_i-f(x_i))^2\)来表示回归树对于训练数据的预测误差，用平方误差最小的准则求解每个单元上的最优输出值.易知，单元\(R_m\)上的\(c_m\)的最优值\(\hat c_m\)是\(R_m\)上的所有输入实例\(x_i\)对应的输出\(y_i\)的均值，即:

    问题是怎样对输入空间进行划分,这里采用启发式的方法，选择第j个变量\(x^{(j)}\)和它取的值s，作为切分变量（splitting variable)和切分点（splitting point),并定义两个区域：

    然后寻找最优切分变量j和最优切分点s，最优地，求解：

    对固定输入变量j可以找到最优切分点s:

    便利所有输入变量，找到最优的切分变量j，构成一个对\((j,s)\).依此将输入空间划分为两个区域。接着，对每个区域重复上述划分过程，直到满足停止条件为止.这样就生成一棵回归树。这样的回归树通常称为最小二乘回归树(least squares regression tree)，现将算法叙述如下：

    最小二乘回归树生成算法：

    2.分类树的生成

    分类树用基尼指数选择最有特征，同时决定该特征的最优二值切分点。

    基尼指数：

    如果样本集合D根据特征A是否取某一可能值a被分割成\(D_1和D_2\)两部分，即：

    基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似。

    图5.7显示二类分类问题中基尼指数Gini(p)、熵（单位比特）之半和分类误差率的关系.横坐标表示概率P，纵坐标表示损失.可以看出基尼指数和 熵之半的曲线很接近，都可以近似地代表分类误差率.

    CART生成算法：

    下面继续用例题来说明该算法：

    根据上表所给的训练数据集，应用CART算法生成决策树。

    CART剪枝

    CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小(模型变简单)，从而能够对未知数据有更准确的预测.CART剪枝算法由两步组成：首先从生成算法产生的决策树\(T_0\)底端开始不断剪枝，直到\(T_0\)的根结点，形成一个子树序列\( {T_0,T_1,...,T_n}\);然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树.

    1.剪枝，形成一个子树序列
    在剪枝过程中，计算子树的损失函数：

    其中，T为任意子树，C(T)为对训练数据的预测误差(如基尼指数)，丨T丨为子树的叶结点个数，\(α \geq0\)为参数，\(C_{\alpha}(T)\)为参数是\(\alpha\)时的子树T的整体损失.参数\(\alpha\)权衡训练数据的拟合程度与模型的复杂度.

    对固定的\(\alpha\), —定存在使损失函数\(C_{\alpha}(T)\)最小的子树，将其表示为\(T_{\alpha}\)。\(T_{\alpha}\)在损失函数\(C_{\alpha}(T)\)最小的意义下是最优的.容易验证这样的最优子树是唯一的.当\(\alpha\)大的时候，最优子树\(T_{\alpha}\)偏小；当\(\alpha\)小的时候，最优子树\(T_{\alpha}\)偏大.极端情况，当\(\alpha\) = 0时，整体树是最优的.当\(\alpha \rightarrow \infty \)时，根结点组成的单结点树是最优的.

    Breiman等人证明：可以用递归的方法对树进行剪枝.将\(\alpha\)从小增大，\(0=\alpha_0<\alpha_1<...<\alpha_n<\infty,\)，产生一系列的区间\([\alpha_i,\alpha_{i+1}),i=0,1,...n;\)，剪枝得到的子树 序列对应着区间\(\alpha \in [\alpha_i,\alpha_{i+1}),i=0,1,...n;\)的最优子树序列\( {T_0,T_1,...,T_n}\),序列中的子树是嵌套的.


    CART剪枝算法：

    2017/3/30

    « Prev Page

    » Next Page

    Copyright © 2017 Powered by LZH,  Theme used GitHub CSS.