逻辑斯谛回归模型、最大嫡模型学习归结为以似然函数为目标函数的最优化问题,通常通过迭代算法求解.从最优化的观点看,这时的目标函数具有很好的性质.它是光滑的凸函数,因此多种最优化的方法都适用,保证能找到全局最优解.常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法.牛顿法或拟牛顿法一般收敛速度更快.
这次主要学习基于改进的迭代尺度法与拟牛顿法的最大熵模型学习算法。(还有梯度下降法,这次不过多学习)
改进的迭代尺度法
改进的迭代尺度法(improved iterative scaling,IIS)是一种最大熵模型学习的最优化算法.
已知最大熵模型为:
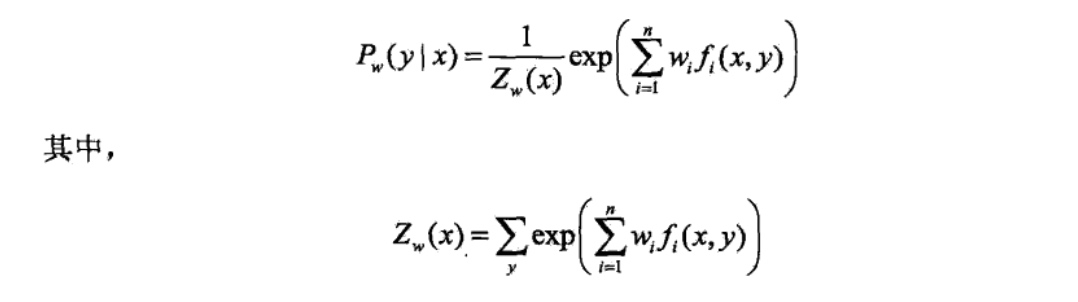
对数似然函数为:
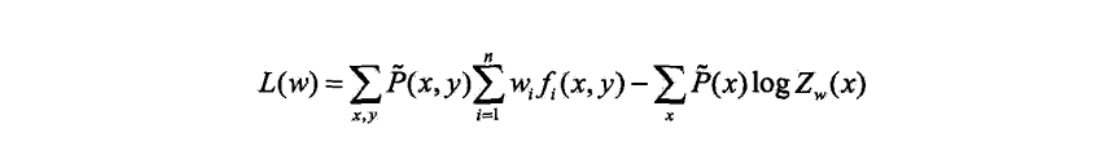
目标是通过极大似然估计学习模型参数,即求对数似然函数的极大值\(\hat{w}\)
改进的迭代尺度算法(iis)的想法是:假设最大熵模型当前的参数向量是\(w=(w_1,w_2,...,w_n)^T\),我们 希望找到一个新的参数向量\(w+\delta = (w_1+\delta_1,w_2+\delta_2,....,w_n+\delta_n)^T\),使得模型的对数似然函数值增大.如果能有这样一种参数向量更新的方法\(\tau:w \rightarrow w+\delta\),那么就 可以重复使用这一方法,直至找到对数似然函数的最大值.
对于给定的经验分布\(\tilde P(x,y)\),模型参数从\(w到w+\delta\),对数似然函数的改变量是:
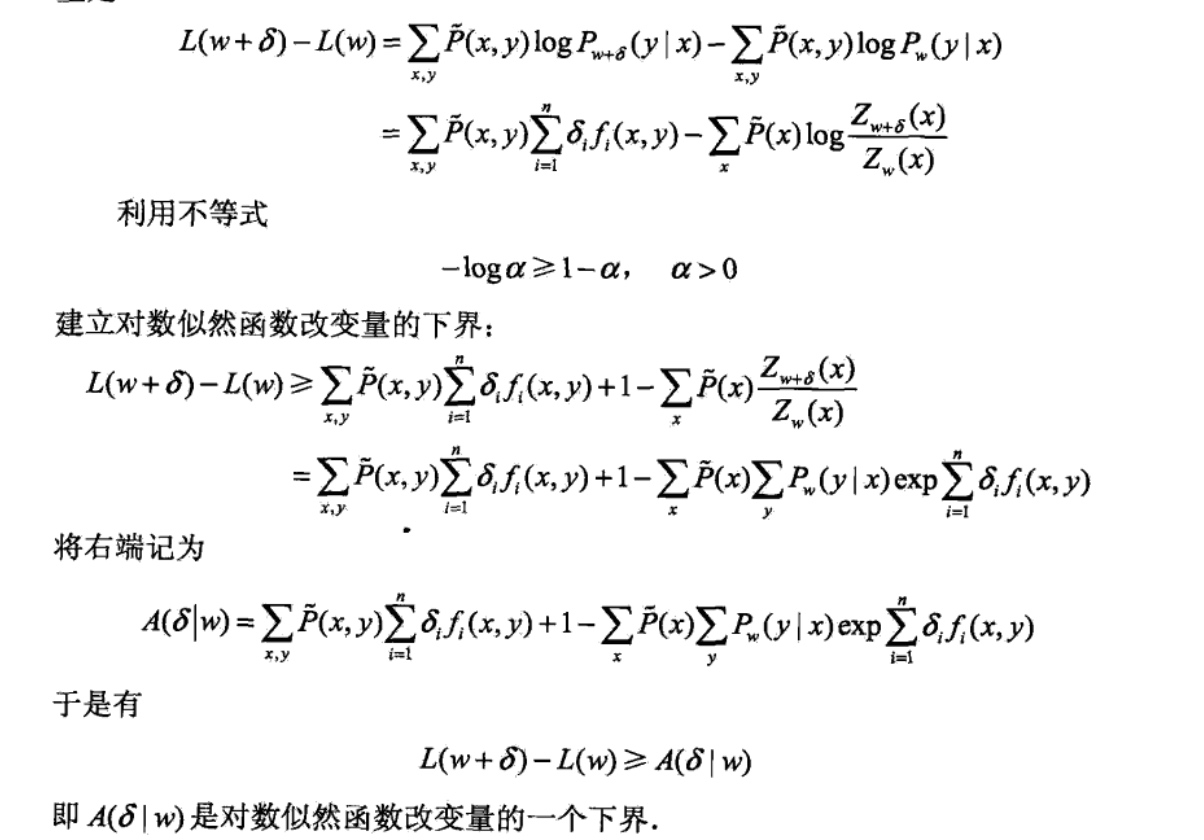
如果能找到适当的\(\delta使下届A(\delta | w)\)提高,那么对数似然函数也会提高。然而,函数\(A(\delta | w)\)中的\(\delta\)是一个向量,含有多个变量,不容易同时优化,IIS试图以此只优化其中一个变量\(\delta_i\),而固定其他变量\(\delta_j,i \neq j\).
为达到这一目的,IIS进一步降低下界\(A(\delta | w)\),具体的,IIS引进一个量\(f^{\#}(x,y)\):
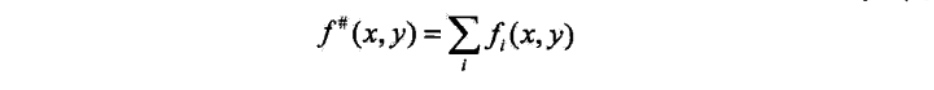
因为\(f_i\)是一个二值函数,故\(f^{\#}(x,y)\)表示所有特征在(x,y)出现的次数,这样,\(A(\delta | w)\)可以改写为:

下面给出IIS算法:


