这个问题是一个典型的可以运用贪心算法的题目，我们在初始的选择一个活动之后，应该将之后的资源被其他任务尽量多的占用。所以我们应该第一个选择活动最快结束的活动，因为它剩下的资源可以被它之后开始的任务尽量多的使用。所以我们可以运用一种递归形式或者迭代算法来表达这个形式：

//
//  main.cpp
//  Greedy_Activity_Selector
//
//  Created by LZH on 2017/11/3.
//  Copyright © 2017年 LZH. All rights reserved.
//

#include <iostream>
#include <vector>
using namespace std;
void print(int n)
{
    cout<<n<<' ';
}

/**
 迭代形式函数

 @param s 活动开始时间数组
 @param f 活动结束时间数组
 @param result  用于存储结果
 */
void GREED_ACTIVITY_SELECTOR(vector<int> s , vector<int> f , vector<int> &result)
{
    int n = s.size();
    result.push_back(1);
    int k=1;
    for (int m=2; m<=n; m++) {
        if (s[m]>=f[k]) {
            result.push_back(m);
            k = m;
        }
    }
}

/**
 尾递归形式函数

 @param s 活动开始时间数组
 @param f 活动结束时间数组
 @param k 从活动k开始计算
 @param n 共有n个活动
 @param result 用于存储结果
 */
void RECURSIVE_ACTIVITY_SELECTOR(vector<int> s,vector<int> f, int k, int n, vector<int> &result)
{
    int m = k+1;
    while (m<=n && s[m]<=f[k]) {
        m++;
    }
    if (m<=n) {
        result.push_back(m);
        RECURSIVE_ACTIVITY_SELECTOR(s, f, m, n ,result);
    }
}

int main() {
    int a[12] ={0,1,3,0,5,3,5,6,8,8,2,12};
    int b[12] ={0,4,5,6,7,9,9,10,11,12,14,16};
    vector<int> s(a,a+12);
    vector<int> f(b,b+12);
    vector<int> result;
    RECURSIVE_ACTIVITY_SELECTOR(s, f, 0, 11, result);
    GREED_ACTIVITY_SELECTOR(s, f, result);
    for_each(result.begin(),result.end(),print);
    return 0;
}

其中递归形式的流程如下图所示：

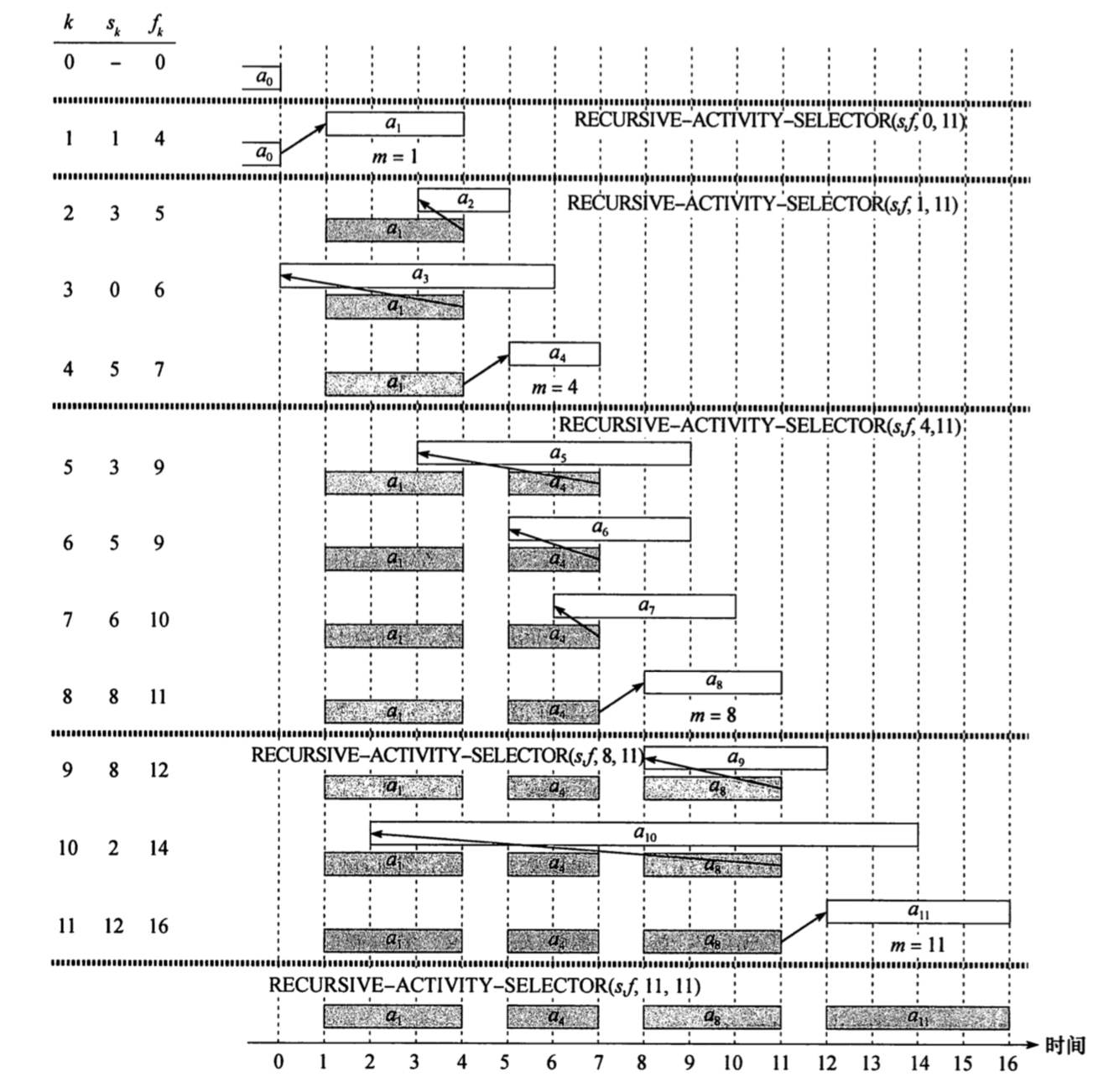
但两种算法运行时间类似都为\(\Theta(n)\)

与动态规划的不同

贪心算法通过做出局部最优来构造全局最优解。换句话说，直接做出在当前问题下看起来最优的选择，而不必考虑子问题的解。

在动态规划中，每个步骤都要进行一次选择，但选择通常依赖于子问题的解，因此，我们通常以自底向上的方式来求解动态规划问题，先求解较小的子问题，然后是较大的子问题。但是在贪心算法中，我们总是做出在当时看起来最佳的选择，然后求解剩下的唯一子问题。贪心算法进行选择时可能依赖之前做出的选择，但不依赖于任何将来的选择或者是子问题的解。所以贪心算法在进行第一次选择时不求解任何子问题，自顶向下进行逐步选择，将给定的子问题实例变小。

两者最典型的区别，可以用分数背包和0-1背包问题来举例，这里不做细说。