Description
Bessie, Farmer John's prize cow, has just won first place in a bovine beauty contest, earning the title 'Miss Cow World'. As a result, Bessie will make a tour of N (2 <= N <= 50,000) farms around the world in order to spread goodwill between farmers and their cows. For simplicity, the world will be represented as a two-dimensional plane, where each farm is located at a pair of integer coordinates (x,y), each having a value in the range -10,000 ... 10,000. No two farms share the same pair of coordinates.

Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms.

Input
Line 1: A single integer, N

Lines 2..N+1: Two space-separated integers x and y specifying coordinate of each farm

Output
Line 1: A single integer that is the squared distance between the pair of farms that are farthest apart from each other.

Sample Input

4
0 0
0 1
1 1
1 0

Sample Output

2

算法思想

流程：

1. 求凸包：最远点对一定在凸包上（可以反证法证之），所以找出凸包后在其上找最远点对就可以少考虑很多点。求凸包可用andrew算法，它是基于graham算法，且更快更稳定。不同于graham算法的逆时针排序，andrew算法采用了点的水平排序，然后分别求下凸包以及上凸包，这样下来整个的凸包便求好了。而且该算法可以解决凸包中有重合点、共线点等问题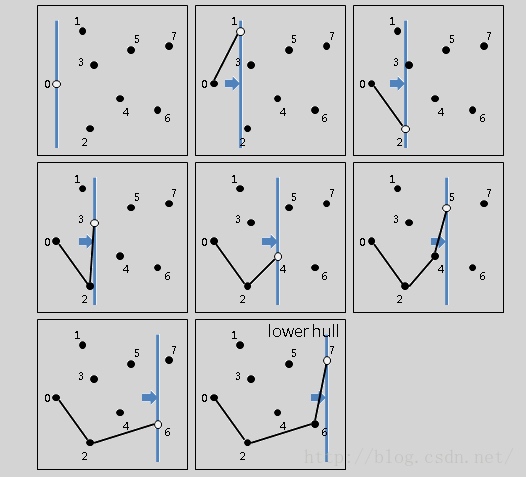

2. 旋转卡壳
   就是两个平行线正好把凸包卡住，其中卡着的点称为对踵点对.
   

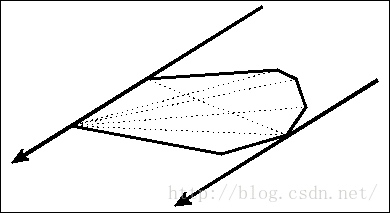
那么怎么才能找到最远点对呢？

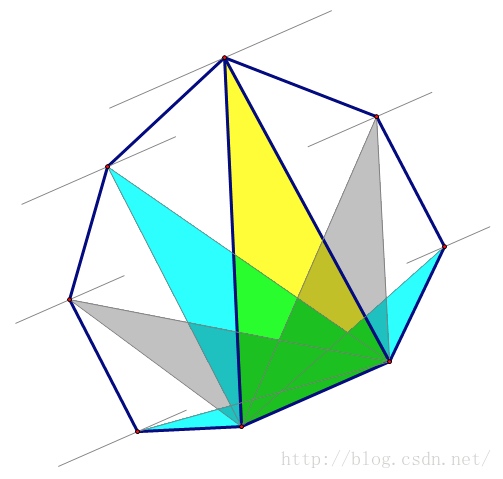
对于上图中的6个三角形的公共底边，可知当三角形的顶点在凸包上按逆时针旋转时，三角形的面积先由小变大再由大变小，即成单峰函数变化。所以在峰值时对应的凸包顶点距底边对应的两个对踵点的距离比其他情况大，这样，枚举每一个边并找到其面积单峰函数峰值对应的顶点，同时更新最大距离，旋转一趟下来便可以得到最后的结果。求面积单峰函数的峰值也很简单，就是通过叉积比较两个三角形的大小，当后者的面积比前者小时便找到了峰值，然后求距离更新最大值即可。

    #include <cstdio>  
    #include <vector>  
    #include <algorithm>  
    #include <cstring>  
    using namespace std;  
    const int maxn = 50000 + 10;  
    typedef int type_xy;  
      
    struct P  
    {  
        type_xy x, y;  
        P() {}  
        P(type_xy x, type_xy y) : x(x), y(y) {}  
        P operator + (P p){ return P(x + p.x, y + p.y); }  
        P operator - (P p){ return P(x - p.x, y - p.y); }  
        P operator * (type_xy d){ return P(x*d, y*d); }  
        bool operator < (const P& a) const  
        {  
            if (x != a.x) return x < a.x;  
            else return y < a.y;  
        }  
        type_xy dot(P p) { return x*p.x + y*p.y; }  
        type_xy det(P p) { return x*p.y - y*p.x; }  
    };  
      
    int N;  
    P ps[maxn];  
      
    //字典序比较  
    bool cmp_x(const P& p, const P& q)  
    {  
        if (p.x != q.x)  
            return p.x < q.x;  
        return p.y < q.y;  
    }  
      
    //求凸包  
    vector<P> convex_hull(P* ps, int n)  
    {  
        sort(ps, ps + n, cmp_x);  
        int k = 0;          //凸包的顶点数  
        vector<P> qs(n * 2);        //构造中的凸包  
        //构造凸包的下侧  
        for (int i = 0; i < n; i++){  
            while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0)  
                k--;  
            qs[k++] = ps[i];  
        }  
        //构造凸包的上侧  
        for (int i = n - 2, t = k; i >= 0; i--){  
            while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0)  
                k--;  
            qs[k++] = ps[i];  
        }  
        qs.resize(k - 1);  
        return qs;  
    }  
      
    //距离的平方  
    double dist(P p, P q)  
    {  
        return (p - q).dot(p - q);  
    }  
      
      
    void solve()  
    {  
        vector<P> qs = convex_hull(ps, N);  
        int n = qs.size();  
        if (n == 2){         //特别处理凸包退化的情况  
            printf("%.0f\n", dist(qs[0], qs[1]));  
            return;  
        }  
        int i = 0, j = 0;           //某个方向上的对踵点对  
        //求出x轴方向上的对踵点对  
        for (int k = 0; k < n; k++){  
            if (!cmp_x(qs[i], qs[k]))  
                i = k;  
            if (cmp_x(qs[j], qs[k]))  
                j = k;  
        }  
        double res = 0;  
        int si = i, sj = j;  
        while (i != sj || j != si){     //将方向逐步旋转180度  
            res = max(res, dist(qs[i], qs[j]));  
            //判断先转到边i-(i+1)的法线方向还是边j-(j+1)的法线方向  
            if ((qs[(i + 1) % n] - qs[i]).det(qs[(j + 1) % n] - qs[j]) < 0)  
                i = (i + 1) % n;        //先转到边i-(i+1)的法线方向  
            else  
                j = (j + 1) % n;        //先转到边j-(j+1)的法线方向  
        }  
        printf("%.0f\n", res);  
    }  
      
    int main()  
    {  
        while (scanf("%d", &N) != EOF){  
            for (int i = 0; i < N; i++){  
                scanf("%d%d", &ps[i].x, &ps[i].y);  
            }  
            solve();  
        }  
        return 0;  
    }